一些简单动态规划的分析 - 张天宇的博客

本文主要记录了一些动态规划的做题技巧、解题步骤，结合LeetCode。

LeetCode 198

小偷计划偷沿街房屋内的现金，相邻的房屋装有相互连通的防盗系统，如果相邻的房屋在同一个晚上被小偷闯入，系统会自动报警。

给定一个代表每个房间金额的非负整数数组，计算在不触动报警装置的情况下，能够偷窃到的最高金额。

示例：输入[1, 2, 3, 1]，输出4。偷了1，3。

解题思路

动态规划四个解题步骤：

定义子问题
写出子问题的递归关系
确定DP数组的计算顺序
空间优化(可选)

代入上面的题目，来看一下运作机制。

定义子问题

子问题：子问题是和原问题相似，但规模较小的问题。例如这道题，从全部房子中能够偷到的最大金额，将问题规模缩小，子问题就是，从k个房子中能够偷到的最大金额，用$f(k)$表示。

所以子问题其实就是将问题参数化。定义的子问题是k，假设有n个房子，就一共有n个问题。这要求子问题具备两个性质：

原问题要能够由子问题表示。比如这道题，k=n的时候就是问题的解，不然的话子问题白解了。
一个子问题的解要能够由其他子问题的解求出。也就是最优子结构，例如本题的解为$f(k)$可以由$f(k-2)$和$f(k-1)$组成。如果没有这个性质，可能没有办法使用动态规划来解。

写出子问题的递归关系

一般来说，直接看当前子问题和前一个子问题的关系。一维问题就是看$f(i)$和$f(i-1)$的关系；如果是二维子问题，则要看$f(i,j)$和$f(i-1,j)$、$f(i-1,j-1)$、$f(i,j-1)$。

这道题中，一共有n个房子，每个房子金额为nums[0],nums[1],…,nums[n-1]，子问题$f(k)$表示偷前k个房子即nums[0],nums[1],…,nums[k-1]。那么偷k个房子其实有两种偷法：

最后一个房子nums[k-1]不偷。那么问题就会变成偷前k-1个房子中偷到最大金额；
偷了第k个房子，那么为了满足题目的要求，第k-1个房子就不能再偷了。那么问题就演变成了前k-2个房子偷到最大的金额。

在这两种情况中选择一个较大的结果，关系式为$f(k) = max(f(k-1), f(k-2)+nums[k-1])$。

在递推关系写完之后，要注意递推关系的跳出条件，也就是基础情况。这道题的基础情况有两种：

当$k=0$时候，即没有房子可以偷，$f(0)=0$；
当$k=1$时候，仅有一个房子，直接偷了这个房子，$f(1) = nums[0]$。

确定DP数组的计算顺序

动态规划一般有两种计算顺序，自顶向下使用备忘录的递归方法；一种是自底向上使用DP数组的循环。

由上边的递推式子可以看到，每个$f(k)$依赖$f(k-1)$和$f(k-2)$，也就是说在数组中，dp[k]依赖dp[k-1]和dp[k-2]。可以看到数组中的依赖方向是一致的，每一个元素都是靠左边的元素计算出来的。DP数组从左往右计算，这意味着我们在计算一个子问题的时候，她所依赖的子问题已经解出来了。

事实上，这里应该要考虑一些DP数组的问题，将在下文1143题中给出。

代码

class Solution {
    public int rob(int[] nums) {
        if (nums.length == 0) return 0;
        int[] dp = new int[nums.length+1];
        dp[0] = 0;
        dp[1] = nums[0];
        for (int i = 2; i <= nums.length; i++){
            dp[i] = Math.max(dp[i - 1], dp[i-2] + nums[i-1]);
        }
        return dp[nums.length];
    }
}

空间优化

这一步是为了减少空间复杂度，作为解题目的来说，可有可无。

空间优化的基本原理是，很多时候我们并不需要始终持有全部的DP数组。例如本题当中，我们实际上只用了前两个结果，再往前的结果我们已经用不到了。所以我们可以只用两个变量来保存子问题的结果。这样空间复杂度就从$O(n)$降到了$O(1)$。

public int rob(int[] nums) {
    int prev = 0;
    int curr = 0;
    // 每次循环，计算「偷到当前房子为止的最大金额」
    for (int i : nums) {
        // 循环开始时，curr 表示 dp[k-1]，prev 表示 dp[k-2]
        // dp[k] = max{ dp[k-1], dp[k-2] + i }
        int temp = Math.max(curr, prev + i);
        prev = curr;
        curr = temp;
        // 循环结束时，curr 表示 dp[k]，prev 表示 dp[k-1]
    }

    return curr;
}

LeetCode 1143

题目大意

给定两个字符串 s 和 t，返回这两个字符串的最长公共子序列的长度。若这两个字符串没有公共子序列，则返回 0。

一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，“ace” 是 “abcde” 的子序列。

解题步骤

定义子问题

原问题是s和t的最长公共子序列。那么子问题可以缩小字符串s和t的规模，变成s的前i个字符和t的前j个字符的最长公共子序列，用$f(i,j)$来表示。

子问题的递推关系

我们可以比较s和t的最后一个字符s[i-1]和t[j-1]。可能会有两种情况：

如果两个字符相等即s[i-1]==t[j-1]，我们可以用这个字符作为最长公共子序列的最左字符，然后找s的前i-1和t的前j-1个字符的公共子序列；
如果两个字符不相等，可以尝试删除s或者t末尾的一个字符，即s的前i-1和t的前i或者s的前i和t的前j-1。再从两种方案中选一个较长的公共子序列。

可以得到子问题的递推关系为：
$$
f(i,j)=
\begin{cases}
f(i-1,j-1) + 1 & if(s[i-1] = t[i-1]) \
max\begin{cases}
f(i-1, j)\
f(i, j-1)
\end{cases} & other
\end{cases}
$$
基础解，当i=0时候，s为空，最长公共子序列为0；同理，j=0，结果也为0。

确定DP数组的计算顺序

确定计算顺序是为了在计算子问题时候他所依赖的子问题已经计算好了。因此需要考虑三个问题：

DP数组的有效范围是什么？
基础解和原问题在DP数组中处于什么位置？
DP数组的子问题依赖方向是什么？

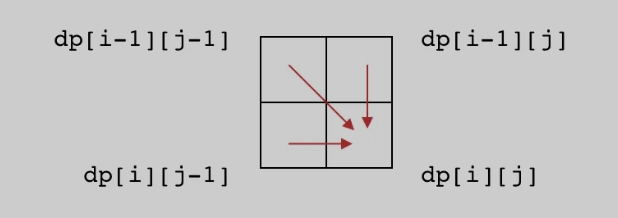
我们发现，子问题的依赖方向是向右、向下的，因此 DP 数组的计算顺序也应该是从左到右、从上到下。也就是说我们应该以这样的顺序遍历 DP 数组。

代码

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        if (text1.isEmpty() || text2.isEmpty()) return 0;
        int m = text1.length();
        int n = text2.length();
        int[][] dp = new int[m+1][n+1];
        for (int i = 0; i <= m; i++){
            for (int j = 0; j <= n; j++){
                if (i == 0 || j == 0){
                    dp[i][j] = 0;
                } else {
                    if (text1.charAt(i-1) == text2.charAt(j-1)){
                        dp[i][j] = dp[i-1][j-1]+1;
                    }
                    else {
                        dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                    }
                }
            }
        }
        return dp[m][n];
    }
}

LeetCode 53

题目大意

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

输入： [-2,1,-3,4,-1,2,1,-5,4]，输出：6。
解释：连续子数组 [4,-1,2,1] 的和最大，为 6。

解题步骤

定义子问题

为了让结果出现子问题特征，我们定义子问题为：$f(k)$表示前k个数中，以最后一个元素结尾的最大子数组和。当$f(4)=3$时，计算$f(5)$时候，直接将新元素4和前面最优解拼接即可，这满足了子问题特征。

注意，这里如果取了这种定义方式，那么最后结果就不能直接返回$f(k)$了，因为它仅代表以第k个数结尾的最大值。我们要取整个数组的最大值。

子问题的递推关系

计算当前最优解，会出现几种情况：最优解+当前位置数字，或者当前数字。这取决于前面最优解是正负和当前位置的正负，对结果的影响。递推公式为：
$$
f(k)= max
\begin{cases}
f(k-1) + nums[k-1] \
nums[k-1]
\end{cases}
$$
简化一下：
$$
f(k) = max(f(k-1), 0) +nums[k-1]
$$

代码

public int maxSubArray(int[] nums) {
	int N = nums.length;
    int[] dp = new int[N+1];
    dp[0] = 0;

    int res = Integer.MIN_VALUE;
    for (int k = 1; k <= N; k++) {
        dp[k] = Math.max(dp[k-1], 0) + nums[k-1];
        res = Math.max(res, dp[k]);
    }
    return res;
}

LeetCode 718

题目大意

给两个整数数组 s 和 t ，返回两个数组中公共的、长度最长的子数组的长度。例如：

输入：s: [1, 2, 3, 2, 1, 5]，t: [6，3, 2, 1, 4, 7]
输出：3
解释：长度最长的公共子数组是 [3, 2, 1]。

解题思路

子序列 (subsequence) 可以是不连续的。例如 “ACD” 是 “ABCDE” 的子序列；
子数组 (subarray)、子串 (substring) 必须是连续的。例如 “BCD” 是 “ABCDE” 的子数组/子串。

定义子问题

根据上一个例子，依旧可以使用数组尾部的限制建立DP数组，将问题定义为，$f(i, j)$表示s[0…i)和t[0…j)中，以最后一个元素结尾的最长公共数组。以最后一个元素结尾指的是公共子数组既要包含 s[0..i) 的最后一个元素，也要包含 t[0..j) 的最后一个元素。也就是说从后往前看，两个数组中的最后几个元素是相同的。

子问题的递推关系

如果s[i-1] == t[j-1]，那么已经有一个元素是相同的，接下来继续往前看s[0…i-1]和t[0…j-1]的最后几个元素是相同的。也就是$f(i,j)=f(i-1,j-1)+1$。
如果s[i-1] != t[j-1]，那么最后一个元素就不相同，前面就不用看了，$f(i,j) = 0$。

可得递推式：
$$
f(i,j)=
\begin{cases}
f(i-1,j-1)+1 & if s[i-1] = t[i-1] \
0 & other
\end{cases}
$$

代码

class Solution {
    public int findLength(int[] A, int[] B) {
        int m = A.length;
        int n = B.length;
        int[][] dp = new int[m+1][n+1];
        int res = 0;
        for (int i = 0; i<=m; i++){
            for (int j = 0; j <= n; j++){
                if (i==0||j==0){
                    dp[i][j] = 0;
                } else{
                    if (A[i-1]==B[j-1]){
                        dp[i][j] = dp[i-1][j-1]+1;
                    } else{
                        dp[i][j] =0;
                    }
                }
                res = Math.max(res, dp[i][j]);
            }
        }
        return res;
    }
}

LeetCode 120

题目大意

给出一个三角形，计算从三角形顶部到底部的最小路径和，每一步都可以移动到下面一行相邻的数字。

1	[↵ [2],↵ [3,4],↵ [6,5,7],↵ [4,1,8,3]↵]

最小的从顶部到底部的路径和是2 + 3 + 5 + 1 = 11。

解题思路

将问题定义为$f(j,j)$，表示以第i行第j个元素为结尾的三角形序列的最小值。利用上下层关系，从上往下从左往右计算即可。最后取最小值。

代码

import java.util.*;
public class Solution {
    public int minimumTotal(ArrayList<ArrayList<Integer>> triangle) {
        int[][] dp = new int[triangle.size()+1][triangle.get(triangle.size()-1).size()+1];
        dp[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < triangle.size(); i++){
            for (int j = 0; j < triangle.get(i).size(); j++){
                if (j == 0){
                    dp[i][j] = dp[i-1][0] + triangle.get(i).get(j);
                } else if (j == triangle.get(i).size()-1){
                    dp[i][j] = dp[i-1][j-1] + triangle.get(i).get(j);
                } else{
                    dp[i][j] = Math.min(dp[i-1][j-1], dp[i-1][j]) + triangle.get(i).get(j);
                }
            }
        }
        int res = Integer.MAX_VALUE;
        for (int i = 0; i < triangle.get(triangle.size()-1).size(); i++){
            if (dp[triangle.size()-1][i] < res) res = dp[triangle.size()-1][i];
        }
        return res;
    }
}

子问题拆分

参考

https://mp.weixin.qq.com/s/TE-p4WYQBBubhxmT137O9w

https://mp.weixin.qq.com/s/e6L2tvWOS_D0obHR_360Gw

LeetCode 198

解题思路

定义子问题

写出子问题的递归关系

确定DP数组的计算顺序

代码

空间优化

LeetCode 1143

题目大意

解题步骤

定义子问题

子问题的递推关系

确定DP数组的计算顺序

代码

LeetCode 53

题目大意

解题步骤

定义子问题

子问题的递推关系

代码

LeetCode 718

题目大意

解题思路

定义子问题

子问题的递推关系

代码

LeetCode 120

题目大意

解题思路

代码

子问题拆分

标签